11231. Коровья
академия 1
Беси учится на
PhD в компьютерных науках. Она опубликовала n статей и её i-ую статью
цитировали ci раз.
Беси слышала что
академические успехи измеряются h-индексом. h-индекс – это наибольшее
число h такое, что ученый имеет не менее h статей, каждая из
которых цитируется не менее h раз. Например, учёный у которого четрые
статьи с количествами цитат (1, 100, 2, 3) имеет h-индекс равный 2,
а ученый с количествами цитат (1, 100, 3, 3) имеет h-индекс равный 3.
Чтобы повысить
свой h-индекс Беси планирует написать обзорную статью, цитирующую
некоторые из её прошлых статей. В связи с ограничением на количество страниц,
она может включить не более l цитат в свой обзор, и конечно же она может
процитировать каждую из своих статей не более одного раза.
Помогите Беси
определить максимальный h-индекс, который она может достичь написанием
своей обзорной статьи.
Заметим, что
научный руководитель должен был предупредить Беси, что написание статьи
исключительно с целью увеличения своего h-индекса сомнительно с этической
точки зрения.
Вход. Первая строка
содержит n (1 ≤ n ≤ 105) и l (0 ≤
l ≤ 105). Вторая строка содержит n целых чисел c1,
.., cn (0 ≤ ci ≤ 105).
Выход. Выведите
максимальный h-индекс, который Беси может получить написанием обзорной
статьи.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 0 1 100 2 3 |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 1 1 100 2 3 |
3 |
РЕШЕНИЕ
жадность
Анализ алгоритма
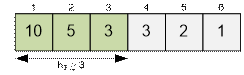
Рассмотрим как
определить h-индекс для заданного массива чисел. Отсортируем его по
убыванию. Теперь следует найти такой наибольший индекс h, что числа,
находящиеся на позициях от 1 до h имеют значения не меньше h.
Ищем такое максимальное h, что ah ≥ h. Например, для следующего примера h-индекс
равен 3, потому что a3 ≥ 3, но a4 < 4.
После включения l
цитат h-индекс не может вырасти больше чем на 1. Действительно,
поскольку ah+1 < h + 1, а каждая
статья может быть процитирована не более одного раза, то максимум что мы можем
сделать – увеличить ah + 1 на 1 если до
этого ah + 1 равнялось h.
Начиная с
индекса h + 1 и в направлении уменьшения индексов будем увеличивать элементы
массива на 1. То есть увеличим на 1 элементы на отрезке a[max(1, h – l + 2); h + 1].
Снова
отсортируем массив по убыванию и вычислим его h-индекс. Это и будет
ответ.
Пример
В первом примере
Беси не может цитировать свои статьи. Её h-индекс для (1, 100, 2, 3) равен 2.
Во втором
примере если Беси процитирует третью статью, её количество цитирований станет
равным (1, 100, 3, 3). В этом случае h равен 3.
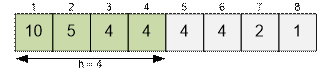
Рассмотрим следующий пример. Числа приведем уже в
отсортированном по убыванию виде. h-индекс массива равен 4.
·
Пусть l
= 2. Увеличим элементы a[4; 5] на 1. Отсортируем массив по убыванию.
h-индекс полученного массива равен 4.

·
Пусть l
= 4. Увеличим
элементы a[2; 5] на 1.
Отсортируем массив по убыванию. h-индекс полученного массива равен 5.

Реализация алгоритма
Функция hIndex вычисляет h-индекс для
массива, уже отсортированного по убыванию. Индексация начинается с 1. Функция возвращает максимальное значение
i, для которого vi ≥ i. Если такого индекса нет (h-индекс массива равен n), то возвращаем
v.size() – 1 =
n.
int hIndex(vector<int> &v)
{
for (int i = 1; i < v.size(); i++)
if (v[i] < i) return i - 1;
return v.size()
- 1;
}
Основная часть программы. Читаем входные данные.
scanf("%d %d", &n, &l);
v.resize(n
+ 1);
for (i = 1; i <= n; i++)
scanf("%d", &v[i]);
Вычисляем h-индекс исходного массива.
sort(v.begin()
+ 1, v.end(), greater<int>());
h =
hIndex(v);
Начиная с позиции h
+ 1 и в
направлении нуля увеличиваем на единицу значения vi.
for (i = h + 1; i > max(h - l + 1,
0); i--)
v[i]++;
Сортируем массив по убыванию и снова вычисляем его h-индекс.
sort(v.begin() + 1, v.end(), greater<int>());
h =
hIndex(v);
Выводим ответ.
printf("%d\n", h);